A. H. Louie
This is a brief introduction to the Rashevsky-Rosen school of relational biology.
Relational biology is the study of biology from the standpoint of ‘organization of relations’. It was founded by Nicolas Rashevsky in the 1950s, thence continued and flourished under his student Robert Rosen. And I was Rosen’s student.

Nicolas Rashevsky
(1899–1972)

Robert Rosen
(1934–1998)
The Modelling Relation
Causality in the modern sense, the principle that every effect has a cause, is a reflection of the belief that successions of events in the world are governed by definite relations. Natural Law posits the existence of these entailment relations and that this causal order can be imaged by implicative order.
A modelling relation is a commutative functorial encoding and decoding between two systems. Between a natural system (an object partitioned from the physical universe) and a formal system (an object in the universe of mathematics) , the situation may be represented in the following canonical diagram:
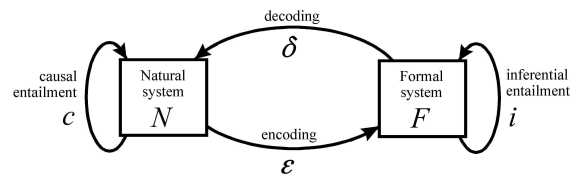
The encoding ε maps the natural system N and its causal entailment c therein to the formal system F and its internal inferential entailment i ; i.e.,
ε : N → F and ε : c → i .
The decoding δ does the reverse. The entailments satisfy the commutativity condition
c = ε ► i ► δ .
Stated graphically, this equality says that, in the diagram above, tracing through arrow c is the same as tracing through the three arrows ε , i , and δ in succession. Thence related, F is a model of N, and N is a realization of F. In terms of the modelling relation, Natural Law is a statement on the existence of causal entailment c and the encodings ε : N → F and ε : c → i .
A formal system may simply be considered as a set with additional mathematical structures. So the mathematical statement ε : N → F , i.e., the posited existence for every natural system N a model formal system F , may be stated as the axiom
Everything is a set.
A mapping is an inference that assigns to each element of one set a unique element of another set. In elementary mathematics, when the two sets involved are sets of numbers, the inference process is often called a function. So ‘mapping’ may be considered a generalization of the term, when the sets are not necessarily of numbers. (The use of ‘mapping’ here avoids semantic equivocation and leaves ‘function’ to its biological meaning.)
Causal entailment in a natural system is a network of interacting processes. The mathematical statement ε : c → i , i.e., the functorial correspondence between causality c in the natural domain and inference i in the formal domain, may thus be stated as an epistemological principle, the axiom
Every process is a mapping.
Together, the two axioms are the mathematical formulation of Natural Law. These self-evident truths serve to explain “the unreasonable effectiveness of mathematics in the natural sciences”.
Biology Extends Physics
A living system is a material system, so its study shares the material cause with physics and chemistry. Reductionists claim this, therefore, makes biology reducible to ‘physics’. Physics, in its original meaning of the Greek word φύσις, is simply (the study of) nature. So in this sense it is tautological that everything is reducible to physics. But the hardcore reductionists, unfortunately, take the term ‘physics’ to pretentiously mean ‘(the toolbox of) contemporary physics’.
Contemporary physics that is the physics of mechanisms reduces biology to an exercise in molecular dynamics. This reductionistic exercise, for example practised in biochemistry and molecular biology, is useful and has enjoyed popular success and increased our understanding life by parts. But it has become evident that there are incomparably more aspects of natural systems that the physics of mechanisms is not equipped to explain. The overreaching reductionistic claim of genericity is thus a misrepresentation and renders it into a falsehood.
Biology is a subject concerned with organization of relations. Physicochemical theories are only surrogates of biological theories, because the manners in which the shared matter is organized are fundamentally different. Hence the behaviours of the realizations of these mechanistic surrogates are different from those of living systems. This in-kind difference is the impermeable dichotomy between predicativity and impredicativity.
Relational Biology
The essence of reductionism in biology is to keep the matter of which an organism is made, and throw away the organization, with the belief that, since physicochemical structure implies function, the organization can be effectively reconstituted from the analytic material parts.
Relational biology, on the other hand, keeps the organization and throws away the matter; function dictates structure, whence material aspects are entailed.
In terms of the modelling relation, reductionistic biology is physicochemical process seeking models, while relational biology is organization seeking realizations. Stated otherwise, reductionistic biology begins with the material system and relational biology begins with the mathematics. Thus the principles of relational biology may be considered the operational inverse of (and complementary to) reductionistic ideas.
Any question becomes unanswerable if one does not permit oneself a large enough universe to deal with the question. The failure of presumptuous reductionism is that of the inability of a small surrogate universe to exhaust the real one. Equivocations create artefacts. The limits of mechanistic dogma are very examples of the restrictiveness of self-imposed methodologies that fabricate non-existent artificial ‘limitations’ on science and knowledge. The limitations are due to the nongenericity of the methods and their associated bounded microcosms. One learns something new and fundamental about the universe when it refuses to be exhausted by a posited method.
The above is a necessarily terse introduction to relational biology. The enthusiasts may want to explore the subject further. A good place to start is my 2009 book More Than Life Itself: A Synthetic Continuation in Relational Biology.